Classification des forces:

1. Forces conservatives: forces dont le travail est indépendant du chemin suivi

1. Forces non-conservatives: forces dont le travail dépend du chemin suivi \(\iff\) forces dissipatives dont le travail \(W\lt 0\)

Exemple de force conservative

1. Le poids:

On pose de \(W_1,W_2,W_3\) le travail de \(\vec P\) sur les trajets \(C_1,C_1,C_3\)
Le poids est constant:
\(\delta W=\vec F.\vec dl\)
\(W=\int\vec F.\vec dl=\vec F\int\vec dl=\vec F.\vec{AB}\)
$$W=\begin{pmatrix}0\\ 0\\ -mg\end{pmatrix}.\begin{pmatrix}x_b-x_a\\ 0\\ z_b-z_a\end{pmatrix}=mg(z_b-z_a)$$
\(\implies\) Le poids est une force conservative
\(W=-[mgz_b-mgz_a]=-[E_p(b)-E_p(a)]\)
\(\implies\) $$W=-\Delta E_{pp}$$
Généralement on écrit:
$$Ep(z)={{mgz+c^{st} }}$$
$$\text{L'énergie potentiel de pesanteur}$$

1. La force de rappel de Hooke

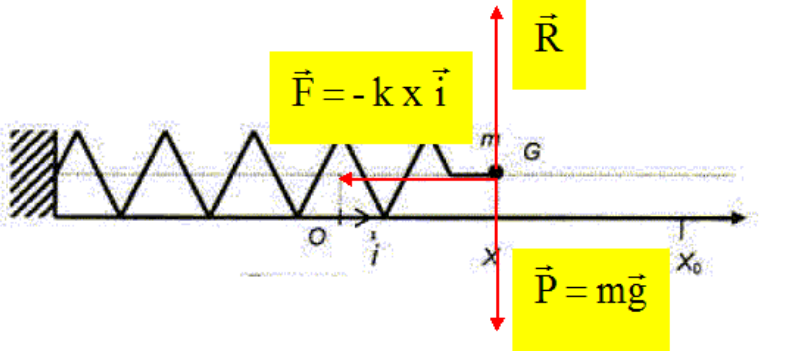\(\vec F_r=-k\,x\,\vec i\)
$$W\int^B_A\vec F \vec {dl}=\int^B_A-kx\vec i$$
$$=-k[\frac{x^2}{2}]^B_A$$
$$=-[\frac 12kx_b^2-\frac 12kx_a^2]$$
$$=-[E_p(B)-E_p(A)]$$
$$W=-\Delta E_p$$ De façon général: \(W={{-\Delta E_p}}\)
A chaque force conservative est associée une énergie potentielle

Energie potentielle

\(W=-\Delta E_p\)
\(\delta W=-dE_p=\vec F.\vec dl\)
\(dE_p=-\vec F.\vec dl\)
$$E_p={{\int-\vec F.\vec dl}}$$
Exemple:

• énergie potentielle de pesanteur:

\(E_{pp}=\int -m\vec g.\vec dl=\int{-\begin{pmatrix}0\\ 0\\ -mg\end{pmatrix}.\begin{pmatrix}dx\\ dy\\ dz\end{pmatrix} }\)
$$E_{pp}(z)=mgz+c^{te}$$

• énergie potentielle élastique-ressort:

\(E_p=\int -(-kx)dx\)
$$E_p=\frac 12 kx^2+C$$

• énergie potentiel d'interaction gravitationnelle:

$$E_p=-G\frac{M.m}r+C$$

De l'énergie potentielle à la force:

\(\vec F=-\overrightarrow{grad}.E_p\)
Un gradient est une variation selon une direction
\(\overrightarrow{grad}\): opérateur différentiel
\(\longrightarrow\) Preuve:
\(\delta W=\vec F.\vec dl=-dE_p\)
\(F.dx=-dE_p\)
\(F=-\frac{dE_p}{dx}\); \(\vec F={{\frac{dE_p}{dx}\vec k}}\)
\(\frac{dE_p}{dx}\): taux d'accroissement de \(E_p\)
\(\frac{dE_p}{dx}\vec k\): gradient de l'\(E_p\) dirigé dans le sens croissant de l'\(E_p\)
$$\frac{dE_p}{dx}\vec k=\overrightarrow{grad}.E_p$$
$$\vec F ={{-\overrightarrow{grad}.E_p}}$$
Si \(E_p(x); \vec F=-\overrightarrow{grad}.E_p={{\frac{dE_p}{dx}\vec e_x}}\)
\(\vec F\) est dirigé dans le sens opposé au gradient de l'Ep, cad dans le sens décroissant de \(E_p\) $$E_p={{\int-\vec F.\vec dl}}$$
$$\vec F={{-\overrightarrow{grad}.E_p}}$$